 Une particularité assez unique du Yocto-Bridge, et de son grand frère le Yocto-MaxiBridge, est la possibilité d'y effectuer une compensation par logiciel de la dérive en température de la cellule de charge. Mais est-ce vraiment nécessaire, et comment s'y prend-on ? Ce sont les questions auxquelles nous allons répondre ici.
Une particularité assez unique du Yocto-Bridge, et de son grand frère le Yocto-MaxiBridge, est la possibilité d'y effectuer une compensation par logiciel de la dérive en température de la cellule de charge. Mais est-ce vraiment nécessaire, et comment s'y prend-on ? Ce sont les questions auxquelles nous allons répondre ici.
Toutes les cellules de charges sérieuses incluent déjà une certaine compensation en température matérielle, sous forme de résistances thermo-sensibles qui corrigent une partie des erreurs de mesure causées par les variations de températures. Pour bien des applications, cela peut suffire. Mais malheureusement, comme le verrons, cette compensation matérielle n'annule pas réellement les variations de mesure causées par la température. D'où l'utilité d'une correction logicielle supplémentaire.
Quand la compensation matérielle suffit
On constate pour commencer que les variations de mesure causées par les changement de température sont en général assez proportionnelles à la température. On peut donc d'emblée admettre que lorsque l'on travaille dans un environnement à température contrôlée, comme une pièce climatisée, le problème n'existera pas.
Deuxième constatation: le principal problème que l'on observe en cas de changement de température est une dérive du zéro. Pour toutes les applications où la balance peut être tarée à zéro juste avant la mesure, la dérive pourra ainsi être contournée.
Ces deux préconditions permettent de couvrir une grande majorité d'applications des cellules de charge sans se poser plus de question.
Quand une compensation supplémentaire est requise
La situation problématique est donc celle où l'on doit peser un objet sans possibilité de tarer la balance, dans un environnement soumis à des fortes variations de température, typiquement à l'extérieur. Un exemple typique est la surveillance de ruches à l'aide de balances automatiques, afin de surveiller l'activité de la colonie et détecter dès que possible un essaimage.
Pour savoir si une compensation supplémentaire est vraiment nécessaire, on peut commencer par regarder la notice de spécification du fabriquant. Par exemple, pour la petite balance de précision que nous vous avions montré à la fin d'un article précédent, le fabricant de la cellule de charge annonce:

Pour une cellule pouvant peser jusqu'à 300g, une erreur de 0.03% * 300g est environ 0.1g par 10 degrés de variation de température. Nous avons donc mis cette balance dans une cloche de protection à l'extérieur, et activé l'enregistreur de données du Yocto-Bridge pour voir ce qu'il en était concrètement durant quelques jours:
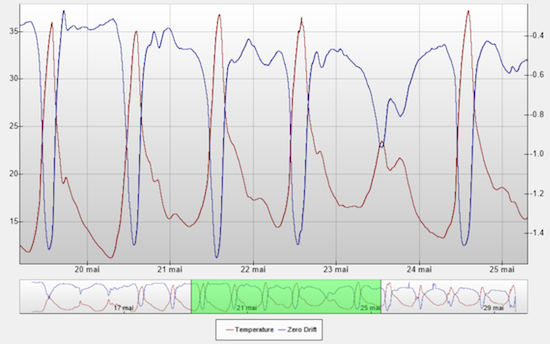
Température et dérive de la tare observée
Première constatation: la dérive de la tare observée est en réalité de l'ordre de 0.5g par 10 degrés, et non 0.1g comme annoncé. Dans le cas de fortes variations de température nuit/jour, cela pourrait conduire à des erreurs de mesure approchant 1%, ce qui devient problématique.
Deuxième constatation: on observe comme mentionné précédemment une très forte corrélation entre l'erreur observée et la température, d'où l'idée d'effectuer une correction logicielle pour améliorer la qualité des mesures. Reste à savoir quelle formule utiliser...
Modélisation de l'erreur
Si on examine plus en détail la corrélation entre la température et la dérive du zéro, on constate que la forme des courbes n'est pas identique. Il ne s'agit donc pas d'une simple dépendance linéaire. Il se produit donc un phénomène qui cause une fluctuation indirecte du poids mesuré à vide. Comme nous n'avons trouvé quasiment aucune littérature documentant les ce phénomène, nous avons fait nos petites expériences numériques et avons découvert que sur toutes les cellules de charge que nous avions, on trouvait dans l'erreur principalement deux composantes:
- Une composante dépendant linéairement de la température moyenne
- Une composante dépendant linéairement de la variation de la température
La dépendance à la variation de température est due soit à une propagation asymétrique de la chaleur dans la cellule de charge, soit à un effet différé dans le temps du mécanisme de compensation en température matériel, qui causerait une erreur différentielle. Voici pour preuve de l’existence de cette composante dépendant de la variation du changement le même graphique que précédemment, mais cette fois avec les variations de températures :
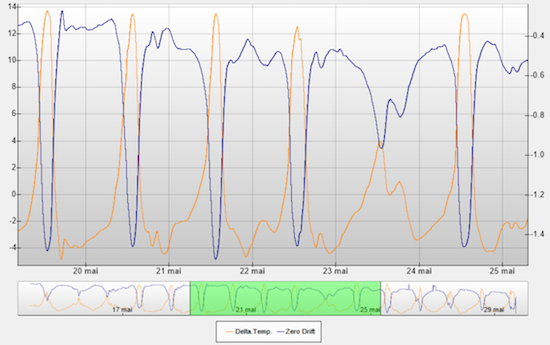
Variation de température et dérive de la tare observée
La ressemblance des courbes est cette fois frappante. Mais pour obtenir une aussi belle ressemblance, il a fallu incorporer un paramètre miracle: l'inertie thermique de la cellule. En effet, les variations de températures n'interviennent pas immédiatement sur la cellule, la chaleur a besoin d'un certain temps pour pénétrer dans la cellule. Nous utilisons une formule typique de la transmission de chaleur vers un matériel:

Cette formule signifie simplement qu'à chaque évaluation, la température de référence pour le calcul de la compensation est calculée comme la valeur précédente ajoutée d'une petite proportion de la différence entre la température extérieure et la température courante. Dans notre cas, on met à jour la température toutes les dix secondes, et on utilise un facteur β d'environ 0.5‰.
Détermination des paramètres de compensation optimaux
Si l'on désire donc soustraire autant que possible l'erreur de mesure due à la température, il va falloir déterminer en fonction du système complet, et de son inertie thermique, quatre paramètres:
- Le coefficient β de transmission thermique pour la variation de température
- La proportion d'erreur causé par la variation de température
- Le coefficient β de transmission thermique pour la température moyenne
- La proportion d'erreur causé par la température moyenne
Le principe consiste donc à installer le système de mesure dans son environnement natif, et d'enregistrer tant la température que le poids à vide en continu, en valeur moyenne 6 fois par minute, pendant une à deux semaines. Comme le Yocto-Bridge est doté d'un enregistreur de données et d'une sonde de température, cela peut être fait très facilement, par exemple avec l'application Yocto-Visualization. On sauve ensuite les données brutes dans un fichier au format CSV pour pouvoir les utiliser pour le calcul.
Il suffit alors d'ouvrir ce fichier avec un petit programme que nous vous avons préparé, et les paramètres nécessaires seront automatiquement calculés, de sorte que vous n'aurez plus qu'à les configurer dans le Yocto-Bridge.

L'outil de calcul des paramètres de compensation en température
Méthode de calcul
Si vous voulez en savoir plus sur le fonctionnement de ce programme, disponible en code source sur GitHub, voici quelques explications de base.
Le premier coefficient de transmission thermique pour la variation de température est le plus coriace à calculer analytiquement. Nous avons donc opté pour une détermination par évaluation itérative: on essaie avec un coefficient de 1‰, 0.9‰, 0.8‰ etc. et lorsqu'on a trouvé le meilleur intervalle on cherche la décimale suivante.
Pour une transmission thermique donnée, il est facile de calculer la proportion d'erreur à appliquer. En effet, comme on s'attend à ce que la dérive du zéro et la variation de température aient des formes identiques, leurs dérivées seront identique aussi, et toutes deux centrées sur le zéro. On calcule donc la proportion absolue des deux courbes, sur la base de leur déviation standard, et la proportion de causalité est connue.
Pour compenser le reste de l'erreur, dépendant de la température moyenne, on soustrait à l'erreur mesurée la correction dépendant de la variation de température précédemment calculée, et on procède à nouveau de la même manière: évaluation itérative du coefficient de transmission thermique, et calcul de la proportion d'erreur par comparaison de la déviation standard.
Nous avons essayé de voir si le résultat pouvait être amélioré par une optimisation multiple des paramètres à l'aide d'une descente de gradient, mais l'effort n'en vaut pas la peine: la méthode ci-dessus donne déjà un résultat quasi-optimal à bien moindre coût.
Conclusion: est-ce que ça marche ?
Le moment de vérité consiste à comparer l'erreur résiduelle à l'erreur originale, pour voir ce que l'on gagne réellement. Pour que le test soit fiable, la détermination des paramètres de compensation par l'outil n'est faite que sur les premiers 75% des mesures. Ainsi, vous pouvez observer sur les 25% suivant comment le système se comporte sur des mesures nouvelles:
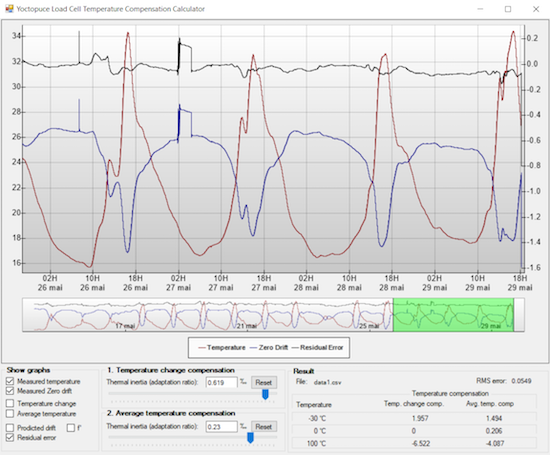
Réduction de l'erreur obtenue par compensation logicielle
On constate que dans le cas présent, la variation du zéro en fonction de la température a pu être divisée d'un facteur 5 à 10 environ. C'est une amélioration typique des résultats que cette méthode permet d'obtenir sur différentes cellules de charge. Dans bien des cas, la différence est donc significative. Par exemple, en regardant le graphique ci-dessus en détail, on observe un petit saut de 0.2g sur la mesure le 27 mai, causé probablement par un insecte qui a du monter sur le plateau de la balance pendant quelques heures. Alors que ce saut était en grande partie masqué par les fluctuations thermiques importantes sur les données originales, il est clairement détectable sur les données améliorées par la compensation logicielle.


