![]() MEMS inertial sensors used in products such as the Yocto-Inclinometer or the Yocto-3D-V2 can determine their orientation with regards to terrestrial gravity, like an electronic spirit level. It is tempting to use them to measure the orientation of moving objects, such as vehicles, but it's not as easy as we might hope. Here are some explanations on the difficulties one might expect, as a reminder of your kinematic physics courses...
MEMS inertial sensors used in products such as the Yocto-Inclinometer or the Yocto-3D-V2 can determine their orientation with regards to terrestrial gravity, like an electronic spirit level. It is tempting to use them to measure the orientation of moving objects, such as vehicles, but it's not as easy as we might hope. Here are some explanations on the difficulties one might expect, as a reminder of your kinematic physics courses...
Let's start with some theory. A MEMS inertial inclinometer works thanks to a tiny mass suspended in an elastic structure. When the inclinometer leans, the mass moves slightly due to the gravity effect. By measuring the movement of the mass by capacitive effect on the three axes, we can deduct the orientation of the gravity vector and thus the module orientation.
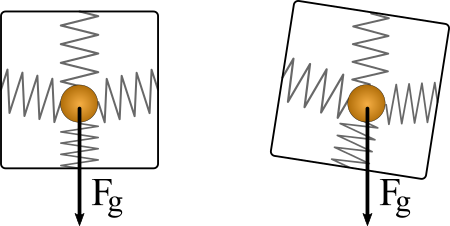
MEMS inclinometer measuring principle
Horizontal acceleration
Obviously, the mass moves not only due to gravity, but also due to all the other forces to which the sensor is subjected. If the sensor is subjected to a horizontal acceleration, the mass moves in the direction opposite to the acceleration, until the elastic return force compensates for the force causing the acceleration. The resulting measured acceleration vector is therefore the sum of the of the gravitational acceleration and the horizontal acceleration. As both vectors are perpendicular, their amplitudes combine with Pythagoras' rule:
The inertial tilt measure, which is based on the angle of the resulting vector, is also distorted. For example, we can compute the fictitious tilt which would be indicated in a car accelerating from 0 to 100km/h in 10 seconds:
So, if you put a Yocto-Inclinometer in an accelerating car and if it tells you that it leans at a 14° angle, no need to change the shocks for all that...
Turn
A similar case happens in a vehicle moving at a constant speed in a turn. Although the vehicle doesn't accelerate, its trajectory turns under the effect of a centripetal force (towards the inside of the bend), caused by the orientation of the directional wheels. Again, the mass of the inclinometer moves in the direction opposite to this force until the elastic return force is equal to it. So we have again a resulting acceleration which is the sum of two perpendicular vectors:

Physics tells us that the centripetal force is proportional to the radius of the turn r and the square of the angular velocity, expressed in radians per second. The resulting centripetal acceleration is given by:
For example, we can compute the perceived acceleration in a car moving at 54km/h in a 25 meter radius highway ramp:
Passengers therefore feels a horizontal acceleration almost equivalent to 1 g. Without surprise, the tilt which would be indicated by a Yocto-Inclinometer, assuming that the vehicle stays perfectly horizontal, is therefore of:
This confirms that you must definitively not trust an inertial inclinometer in a vehicle which follows a curved trajectory. Imagine the result if you wanted to keep a drone horizontal in this way :-)
Experiment with an inclinometer
Yoctopuce modules help you to easily create a small experiment to check the theory. We mounted a bicycle wheel horizontally and we attached to it on a wooden rod:
- a Yocto-3D-V2 containing, among other things, an accelerometer, a gyroscope, and an electronic compass
- a Yocto-Inclinometer, which is a pure and simple MEMS inclinometer
- a YoctoHub-Wireless-n, to transmit the data, without cables getting tangled up
- a USB battery, to power everything
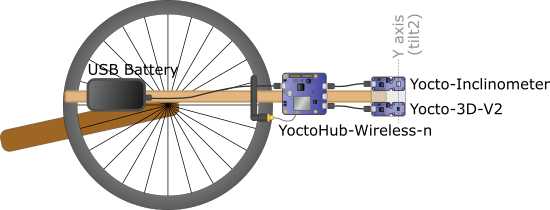
Test system to measure the centripetal force
The wheel is mounted through its axis on a slab. We first put it vertically to balance the wheel: by moving the battery and by adding weights in the rim, we made sure that it stayed motionless in all positions. Then, we mounted it horizontally on a table for the duration of the experiment, so that it can rotate freely and evenly.

Experiment to measure the centripetal force
The experiment consists in launching the wheel manually, and in looking for the resulting measures on the tilt measuring axes of the Yocto-Inclinometer as the wheel decelerates. During the experiment, the gyroscope of the Yocto-3D-V2 (in red) tells us the angular speed of the wheel, while its compass (in orange) enables us to visualize rotation periods:
Perceived tilt measures on a decelerating wheel
Straight off, we can observe two phenomena:
- Small oscillations (+-1°) on the two axes of the inclinometer, in phase with rotation periods, undoubtedly due to a default in the alignment of the wheel with regards to the vertical, which has the effect of leaning the inclinometer sometimes slightly to the top, sometimes slightly to the bottom.
- As expected, a strong influence of the rotation speed on the perceived tilt around the Y axis (Tilt2), of which we check the value below.
To do the numerical checks, we start the wheel again even faster, and this time we display the total acceleration measured by the Yocto-3D-V2 (in gray):
Perceived acceleration on a decelerating wheel
The quadratic dependence of the perceived acceleration on the rotation speed is obvious. Let's check if the values correspond to the theory, for example at the point marked by the vertical marker.
To begin, we must convert the measures of the Yoctopuce module, expressed in current units, in values expressed in SI units used in physics. The gyroscope returns an angular speed in degrees per second, that we must convert in gradients per second:
Likewise, the accelerometer returns a perceived acceleration relative to the value when idle. If we calibrated the sensor, the value when idle would be 1g. In our case, the value when idle is 0.978, we can therefore compute the physical value of the perceived acceleration as follows:
But, as seen previously, the total perceived acceleration in the combination of two perpendicular accelerations: the acceleration due to the centripetal force and the acceleration due to gravity.
By substituting the measured values in this formula, we can therefore deduce the radius of curvature of the trajectory:
And it's actually the rotation radius of our experiment, with an accuracy of about 1%. We could not have hoped for better!
By the way, let's note that as the Yocto-3D-V2 can measure the angular speed and compute the rotation radius, we could even in this precise case compute the travel speed. The case of a uniform circular motion is thus a notable exception to our indication in a previous post that it wasn't possible to measure in a reliable manner the travel speed of an object with a Yocto-3D-V2.
Let's come back to the tilt measure. You may have noticed that the selected computation point corresponds to where the centripetal force is about the same as the gravity force. The perceived tilt measured by the Yocto-Inclinometer should therefore be of about 45°, which is almost the case. Why is it slightly below?
We find the answer in the first graph: there you can notice that there is a slight offset on Tilt1, similar to Tilt2. We could imagine that this offset, indicating a force collinear with the tangent of the circle, corresponds to the deceleration of the wheel. But if you look at the beginning of the graph, you see that the offset is in the same direction as the first impulse, which therefore doesn't correspond to a deceleration. By launching the wheel in the other direction, we can verify that the offset doesn't change sign. Therefore, we must conclude that it is actually a small part of the centripetal acceleration ends up in Tilt1 rather than Tilt2. Why? Simply because of a small flaw in the design of our experiment: our wood rod cannot go exactly through the center of the axis, and the Yocto-Inclinometer is also shifted by 2cm with regards to the rod. As a consequence, the inclinometer ends up twisted 4 degrees with respect to a perfect line going from the sensor to the center of the wheel. Thus a small part of the centripetal force ends up in Tilt1 and a part is missing in Tilt2.
Experiment with a "smart" inclinometer
Finally, let's repeat the experiment by using the tilt measure of the Yocto-3D-V2 rather than the one provided by the Yocto-Inclinometer to see if the result is the same:
Perceived tilt measures with the Yocto-3D-V2
Here is a rather surprising result. For the first 20 seconds, the tilt measure of the Yocto-3D-V2 is not perturbed by the centripetal force. Why? Because, as the BNO055 sensor of the Yocto-3D-V2 is equipped with a gyroscope, it is able to know that it has not been rotated on the Y axis, and therefore that the perceived tilt is not real.
But after 20 seconds, the sensor fusion algorithm seems to decide that the persistent discrepancy between the gyroscope and the inertial inclinometer is finally due to a drift of the gyroscope, and suddenly changes its behavior to integrate the centripetal force in the tilt measurement, even though nothing has changed in the external influences. Again, if it was a matter of keeping an aircraft horizontal, this unexpected effect would make it suddenly go sideways for no reason... Here is a strong reminder of our previous observations of the BNO055 compass, which also suddenly changed behavior during a prolonged discrepancy between the gyroscope and the compass measures.
Conclusion
Before blindly trusting a smart sensor, take care to understand the physics on which it depends and the limits to which it can't escape. Sometimes, it's better to trust a sensor without compensation but predictable, such as the Yocto-Inclinometer, rather than a sensor incorporating compensation mechanisms which are not fully specified. And don't forget that if the Yocto-3D-V2 costs a hundred times less that an inertial station, it's probably because it too has its limits :-)


